Основные круговые кривые описывают дугами окружности, т.е. кривыми постоянной кривизны. Переход с прямого участка на круговую кривую должен совершаться постепенно на протяжении определенного отрезка. Траектория движения автомобиля на подходах к круговой кривой представляет собой кривую, радиус которой постепенно уменьшается от бесконечности (на прямой) до радиуса круговой кривой.
В случае быстрого перехода автомобиля с прямой на кривую центробежная сила в короткий промежуток времени достигает опасной величины, что по своему эффекту соответствует боковому заносу.

В целях безопасности движения при высоких расчетных скоростях и на кривых малых радиусов с обоих концов круговой кривой устраивают переходные кривые, которые представляют собой кривые переменного радиуса. Предусматривают переходные кривые, когда радиусы круговых кривых не превышают 2000 м.
Переходные кривые должны удовлетворять следующим требованиям: в начале переходной кривой, считая е началом конец прямой, радиус кривизны равен бесконечности и затем постепенно уменьшается, приближаясь к радиусу круговой кривой. Такое уменьшение должно происходить постепенно.
В качестве переходных кривых могут быть использованы различные математические кривые, которые удовлетворяют приведенным требованиям. Чаще других применяют клотоиду- математическую кривую, представляющую собой спираль, радиус кривизны которой изменяется непрерывно от р = оо в начальной точке до р = 0 в конце. В качестве переходной кривой или самостоятельного дорожного закругления используют лишь начальный участок клотоиды от р=о до р=< 1 на расстоянии L от начала клотоиды (рис. 12). Переходная кривая, располагаясь внутри угла поворота, вызывает сдвижку основной круговой кривой (рис. 13). При устройстве переходных кривых круговую кривую сохраняют только на протяжении угла а, уменьшенного на 2(3, т.е. центральный угол круговой кривой будет равен а-2< 3, где <3 - угол, образованный касательными в начале и конце переходной кривой. Согласно рис. 13 разбивка переходной кривой возможна лишь при условии 2< 3 <Са. Радиус кривизны обратно пропорционален длине дуги 5 (см. рис. 12)

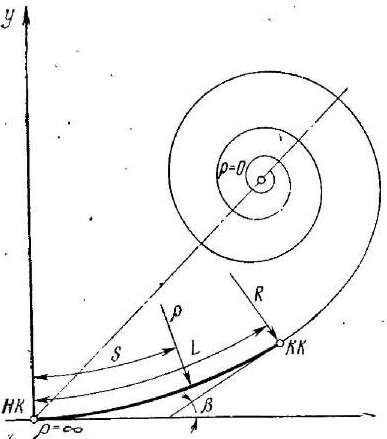
рис. 12

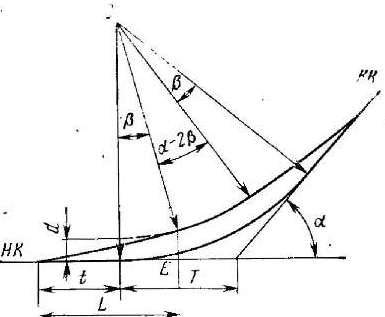
рис. 13